√99以上 ニュートン 微分��程式 193338-ニュートン 冷��法則 微分方程式
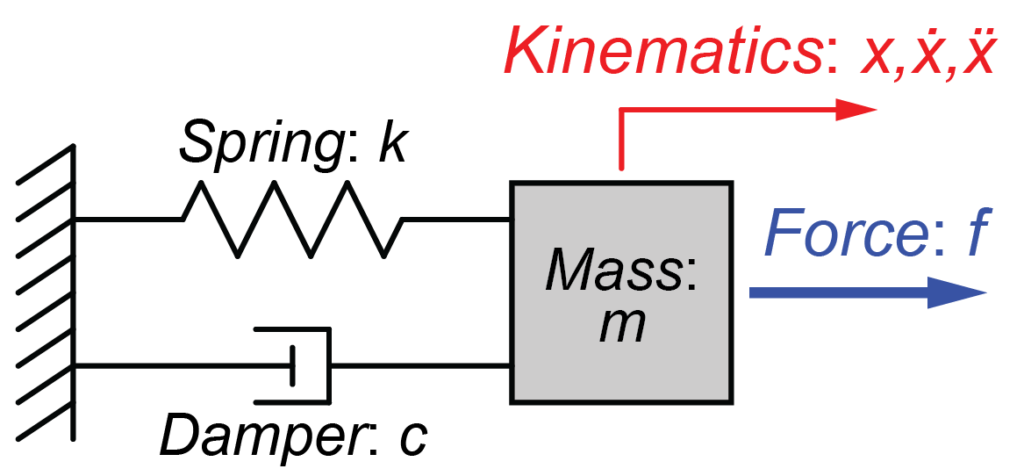
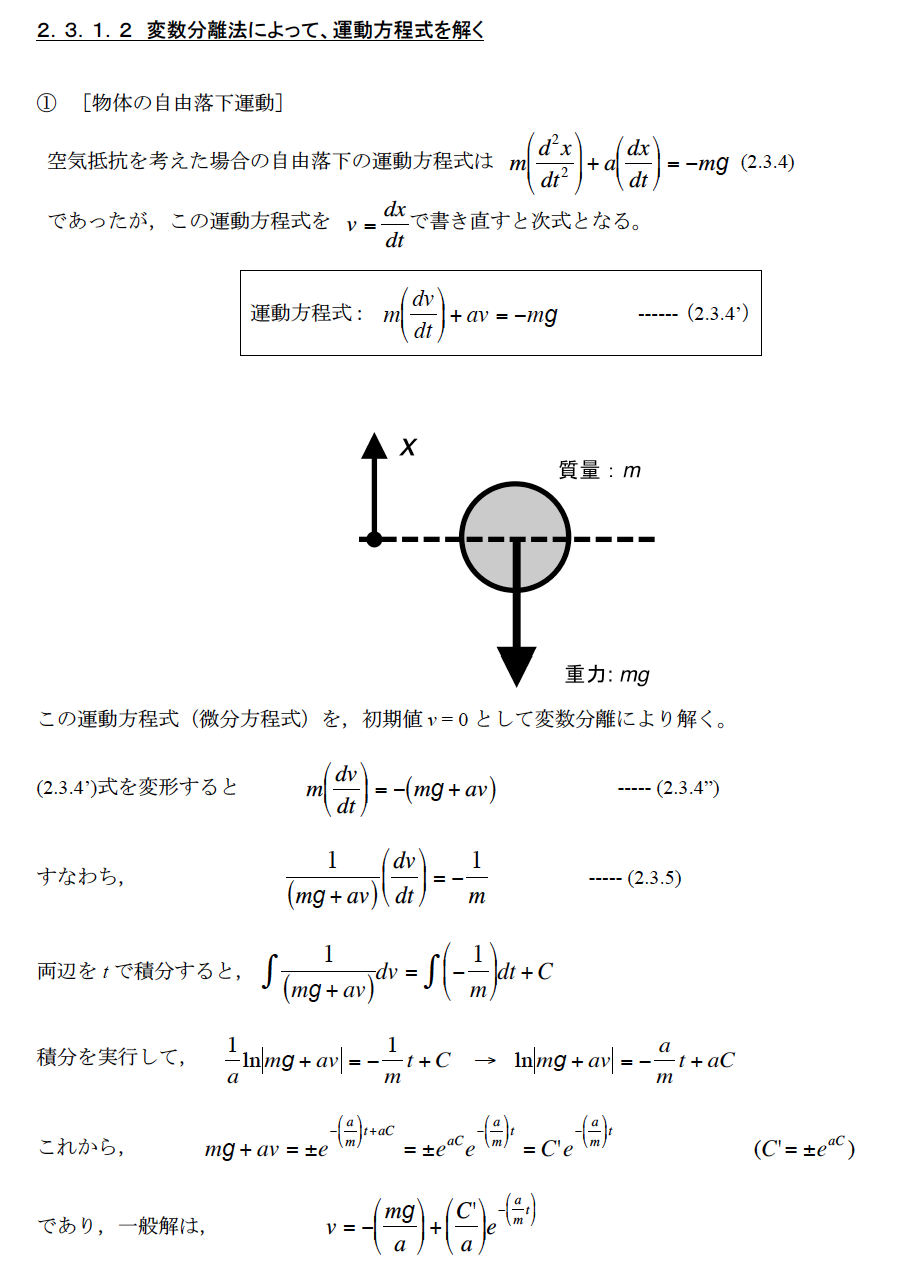
連立1階微分方程式へ変形 ¶ ニュートン方程式は2階の微分方程式ですが、SciPyなど多くのライブラリは連立1階微分方程式 を解くように設計されています( 常微分方程式の解法 を参照) 。そこで、ニュートン方程式を連立1階微分方程式の形に書き換えます。
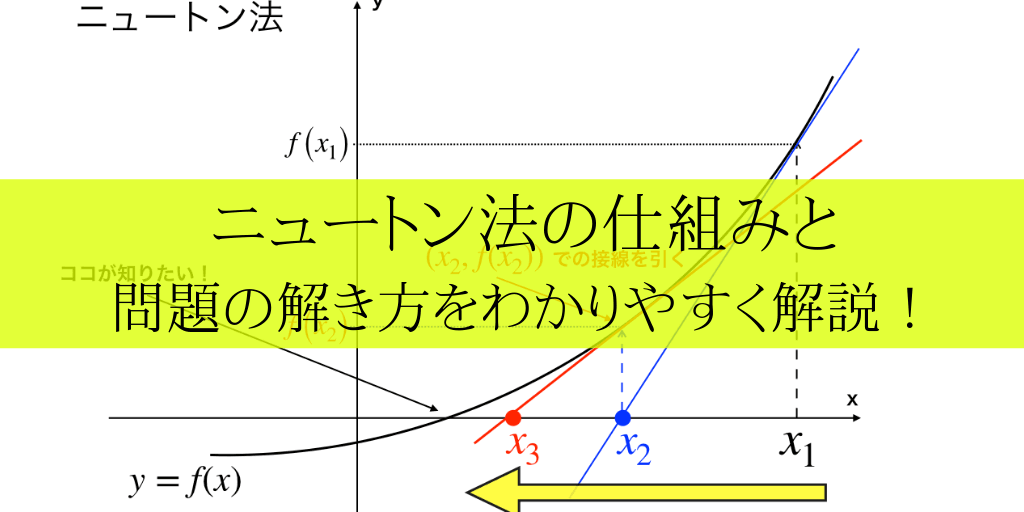
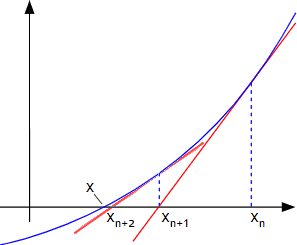
ニュートン 冷却法則 微分方程式-ニュートン法(ニュートン・ラフソン法) とは︖ 非線形方程式f(x) = 0 を数値的に解く方法の1つ 微分可能な方程式であれば、たとえ微分しなくても解が求まる 繰り返し計算により解に近づく 初期値を変えて何回か解く方がよい 1 うさぎでもわかる微分方程式 Part05 2階線形微分方程式の基礎(解の構造・ロンスキアン) こんにちは、ももやまです。 今回から2階以上の線形微分方程式(基本は2階)の解き方や仕組みについて説明していきたいと思います。
ニュートン 冷却法則 微分方程式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | 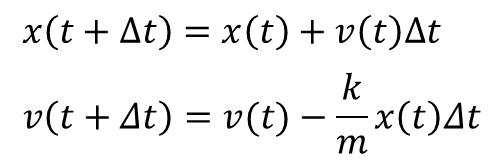 |
 |  |  |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
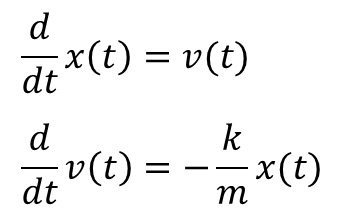 |  | |
 |  | |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
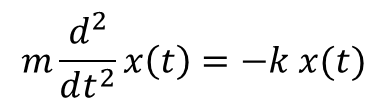 |  | |
 | ||
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 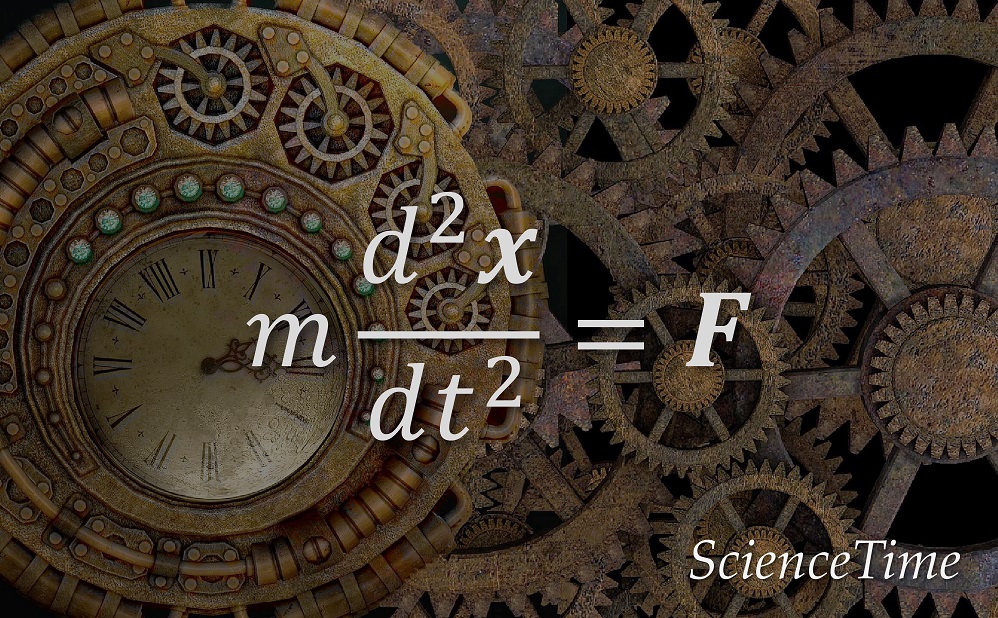 |
 | ||
 |  | |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「ニュートン 冷却法則 微分方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 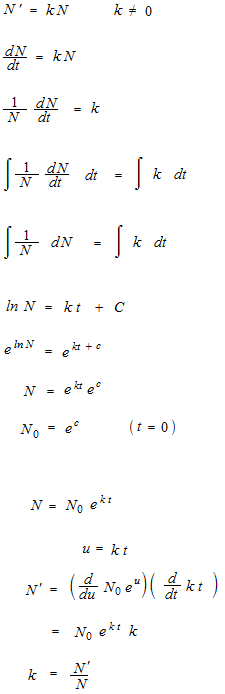 |  |
 |  |  |
 |  |
§25 ニュートンの運動方程式と不定積分 81 §25 ニュートンの運動方程式と不定積分 ニュートンの運動方程式は『プリンキピア』(1687) の中で述べられた運動 の第2 法則(☞p61)にその起源がある:運動の量(=質量m ×速度 v)の 変化(=質量m ×加速度 a)( a(t) = d v(t) dt) は,加えられた力 前回紹介したニュートン・ ラフソン法を利用して, 方程式の解を求めてみましょう。 練習問題ですから, シンプルで, 手でも計算が可能な方程式を取り上げます。 問題の方程式を因数分解をするとわかりますが, 解は重解で1つのみです。 数値計算して得た結果と, 因数分解して得た結
Incoming Term: ニュートン 微分方程式, ニュートン 冷却 微分方程式, ニュートン 冷却法則 微分方程式,
コメント
コメントを投稿